Lines and Angles ⇒⇒ Exercise 6.1

Question 1

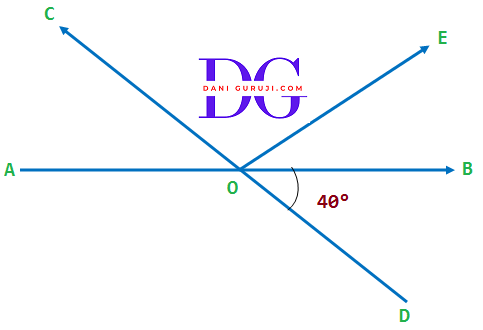
In the figure, lines AB and CD intersect at O . If $ \angle $ AOC + $ \angle $ BOE = 70° and $ \angle $ BOD = 40°, find $ \angle $ BOE and reflex $ \angle $ COE.

Solution :

Given, $ \angle $ AOC + $ \angle $ BOE = 70° and $ \angle $ BOD = 40°

OA and OB are opposite rays, Therefore AB is a line.

Since ray OC stands in a straight line AB

( ∵ Sum of linear pair is always 180° )

∴ $ \angle $ AOC + $ \angle $ BOC = 180°

Calculate $ \angle $ COE

⇒ $ \angle $ AOC + $ \angle $ COE + $ \angle $ BOE = 180°

( ∵ $ \angle $ BOC = $ \angle $ COE + $ \angle $ BOE )

⇒ ($ \angle $ AOC + $ \angle $ BOE )+ $ \angle $ COE = 180°

( ∵ Given, $ \angle $ AOC + $ \angle $ BOE = 70° )

⇒ 70° + $ \angle $ COE = 180°

⇒ $ \angle $ COE = 180° - 70° = 110°

Calculate Reflex $ \angle $ COE

( The sum of all angles around a Point is equal to 360° )

Now, Reflex $ \angle $ COE = 360° - $ \angle $ COE

∴ Reflex $ \angle $ COE = 360° - 110° = 250°

Calculate $ \angle $ BOE

⇒ Now, OC and OD are opposite rays, Therefore CD is a line.

Since ray OE stands in a straight line CD

⇒ $ \angle $ COE + $ \angle $ BOE + $ \angle $ BOD = 180°

( ∵ Sum of linear pair is always 180° )

⇒ 110° + $ \angle $ BOE + 40°= 180°

( ∵ $ \angle $ COE = 110° proved above and Given, $ \angle $ BOD = 40° )

⇒ 150° + $ \angle $ BOE = 180°

⇒ $ \angle $ BOE = 180° - 150°

⇒ $ \angle $ BOE = 30°

Hence, $ \angle $ BOE = 30° and Reflex $ \angle $ COE = 250°

Question 2

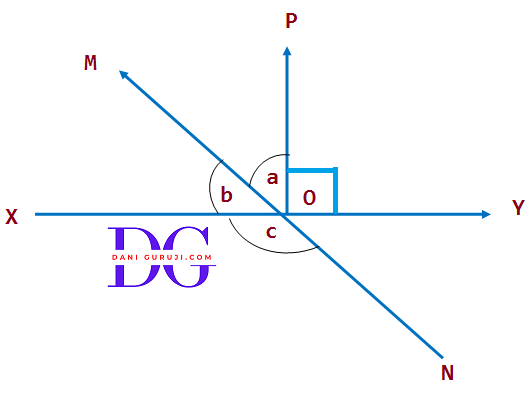
In the figure, lines XY and MN intersect at O. If $ \angle $ POY = 90° and a: b = 2 : 3, find c

Solution :

Given, a: b = 2 : 3 and $ \angle $ POY = 90°

OX and OY are opposite rays, Therefore XY is a line.

Since ray OP stands in a straight line XY

( ∵ Sum of linear pair is always 180° )

Calculate $ \angle $ XOP

∴ $ \angle $ XOP + $ \angle $ POY = 180°

( ∵ Given, $ \angle $ POY = 90° )

∴ $ \angle $ XOP = 180° - 90° = 90°

( ∵ $ \angle $ XOP = $ \angle $ XOM + $ \angle $ MOP )

⇒ $ \angle $ XOM + $ \angle $ MOP = 90°

⇒ b + a = 90°

2. Find the values of a and b using the ratio

Since a and b are in the ratio 2 : 3

∴ Let a = 2x and b = 3x

⇒ 2x + 3x = 90°

⇒ 5x = 90°

⇒ x = 18°

Now, since a = 2x , Substituting value of x

⇒ a = 2 × 18°

⇒a = 36°

Now, since b = 3x , Substituting value of x

⇒ b = 3 × 18°

⇒b = 54°

3. Find the value of c

Now, Since ray OX stands in a straight line MN

$ \angle $ XOM + $ \angle $ XON = 180°

( ∵ Sum of linear pair is always 180° )

( ∵ $ \angle $ XOM = b and $ \angle $ XON = c )

⇒ b + c = 180°

( ∵ $ \angle $ XOM = b = 54° proved above )

⇒ 54° + c = 180°

⇒ c = 180° - 54° = 126°

Answer c = 126°

Question 3

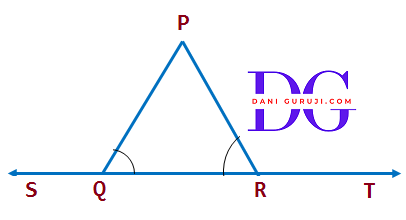
In the figure, $ \angle $ PQR = $ \angle $ PRQ, then prove that $ \angle $ PQS = $ \angle $ PRT.

Solution :

Given, $ \angle $ PQR = $ \angle $ PRQ

To prove, $ \angle $ PQS = $ \angle $ PRT

QS and QR are opposite rays, Therefore SR is a line.

Since ray QP stands in a straight line SR

( ∵ Sum of linear pair is always 180° )

∴ $ \angle $ PQS + $ \angle $ PQR = 180° .. ... (i)

Similarly RT and QR are opposite rays, Therefore QT is a line.

Since ray RP stands in a straight line QT

( ∵ Sum of linear pair is always 180° )

∴ $ \angle $ PRQ + $ \angle $ PRT = 180° ......(ii)

Now, from equation (i) and equation (ii)

⇒ $ \angle $ PQS + $ \angle $ PQR = $ \angle $ PRQ + $ \angle $ PRT

( ∵ Given, $ \angle $ PQR = $ \angle $ PRQ, Now, substituting $ \angle $ PQR at the place of $ \angle $ PRQ in above expression )

⇒ $ \angle $ PQS + $ \angle $ PQR = $ \angle $ PQR + $ \angle $ PRT

⇒ $ \angle $ PQS + $ \angle $ PQR - $ \angle $ PQR = $ \angle $ PRT

⇒ $ \angle $ PQS = $ \angle $ PRT

Hence Proved,

Question 4

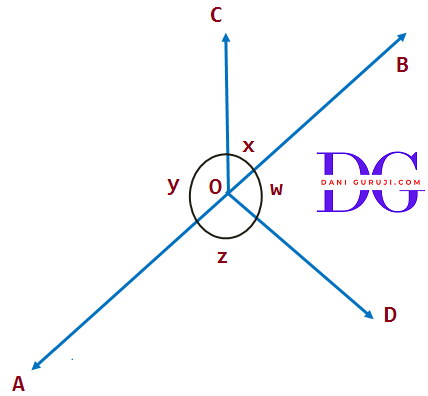
In the figure,if x + y = w + z, then prove that AOB is a line.

Solution :

Given, x + y = w + z

To prove : AOB is a line

$ \angle $ x + $ \angle $ y + $ \angle $ w + $ \angle $ z = 360°

( ∵ The sum of all angles around a Point is equal to 360° )

∴ (x + y )+ (x + y ) = 360°

( ∵ Given, x + y = w + z )

⇒ 2x + 2y = 360°

⇒ 2(x + y) = 360°

⇒ x + y = 180°

Therefore, x and y form a linear pair.

Hence, AOB is a straight line. Proved.

Question 5

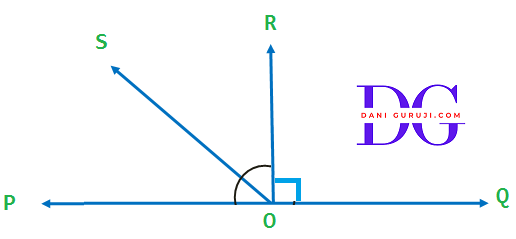
In the figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that $ \angle $ ROS = 1/2 ($ \angle $ QOS – $ \angle $ POS)

Solution :

Given, OR is perpendicular to PQ

To prove : $ \angle $ ROS = 1/2 ($ \angle $ QOS – $ \angle $ POS)

According to the question,

$ \angle $ POR = $ \angle $ QOR = 90°

( ∵ OR is perpendicular to line PQ )

$ \angle $ POR = $ \angle $ QOR

( ∵ $ \angle $ POR = $ \angle $ POS + $ \angle $ ROS )

( ∵ $ \angle $ QOR = $ \angle $ QOS - $ \angle $ ROS )

⇒ $ \angle $ POS + $ \angle $ ROS = $ \angle $ QOS - $ \angle $ ROS

⇒ 2($ \angle $ ROS) = $ \angle $ QOS - $ \angle $ POS

⇒ $ \angle $ ROS = 1/2($ \angle $ QOS - $ \angle $ POS)

Hence Proved.

Question 6

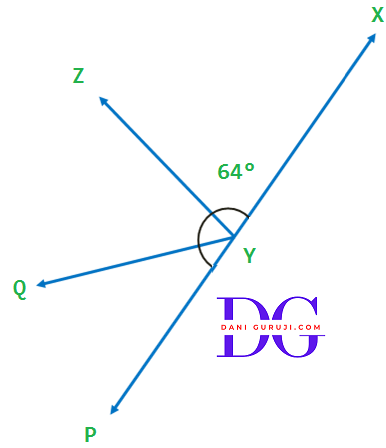
t is given that $ \angle $ XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects $ \angle $ ZYP, find $ \angle $ XYQ and reflex $ \angle $ QYP.

Solution :

Given, $ \angle $ XYZ = 64° . And A ray YQ bisects $ \angle $ ZYP

XY is produced out to point P .

Since ray YZ stands in a straight line XP

( ∵ Sum of linear pair is always 180° )

∴ $ \angle $ XYZ + $ \angle $ ZYP = 180°

(∵ Given, $ \angle $ XYZ = 64° )

⇒ 64° + $ \angle $ ZYP = 180°

⇒ $ \angle $ ZYP = 180° - 64°

⇒ $ \angle $ ZYP = 116°

Since YQ bisects $ \angle $ ZYP

( ∵ $ \angle $ ZYQ = $ \angle $ QYP )

∴ $ \angle $ ZYQ = $ \angle $ QYP = 116°/ 2

Therefore, $ \angle $ ZYQ = $ \angle $ QYP = 58°

Now, $ \angle $ XYQ = $ \angle $ XYZ + $ \angle $ ZYQ

⇒ $ \angle $ XYQ = 64° + 58°

⇒ $ \angle $ XYQ = 122°

Now, reflex $ \angle $ QYP

⇒ 360° - $ \angle $ QYP

( ∵ $ \angle $ QYP = 58° proved above )

⇒ 360° - 58°

Reflex $ \angle $ QYP = 302°